Chapter 4 特征分解 {Eigen decomposition}
4.1 出现原因
4.1.1 主成分分析
eigen是如此的重要,之前我已经写过一篇文章了特征值与特征向量,现在我们来看一下它可能会出现的场合,假设我有一堆 \(\mathbf{x}_i\), 我们想要找到它的主成分:
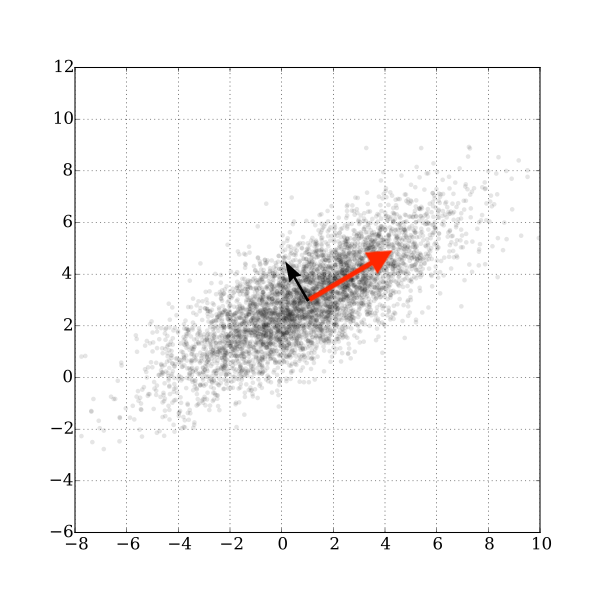
图片来自wikipedia
比如就像图中,我们想找到红色箭头方向 \(\mathbf{v}_i\) ,那么我们可以列出方程:
\[ \text{minimize} \sum_i || \mathbf{x}_i − \text{proj}_{\mathbf{v}} \mathbf{x}_i||^2 \\ || \mathbf{v} || = 1 \]
加上 \(|| \mathbf{v} || = 1\) 假设 \(\mathbf{v}\) 为单位向量,方便计算,所以:
\[ \begin{aligned} \sum|| \mathbf{x}_i − \text{proj}_{\mathbf{v}} \mathbf{x}_i||^2 {} &= ||\mathbf{x}_i − (\mathbf{x}_i \cdot \mathbf{v})\mathbf{v}) ||^2 \\ &= ||\mathbf{x}_i||^2 - 2 (\mathbf{x}_i \cdot \mathbf{v})^2 + (\mathbf{x}_i \cdot \mathbf{v})^2\\ &= ||\mathbf{x}_i||^2 - (\mathbf{x}_i \cdot \mathbf{v})^2\\ \end{aligned} \]
最小化上面这个式子,其中 \(\mathbf{x}_i\) 是已知,我们要求 \(\mathbf{v}\) ,第一项固定,那么我们也就是最大化:
\[ \sum_i (\mathbf{x}_i \cdot \mathbf{v})^2 \]
那实际上也就是我们需要最大化:
\[ ||X^T\mathbf{v}||^2\\ || \mathbf{v} || = 1 \]
这里还是比较容易想清楚的,我们用 \(\mathbf{x}_i\) 来点乘 \(\mathbf{v}\), 然后要它们加起来和最大,每一项当然都要求大,我们就可以写成矩阵形式 \(X^T\mathbf{v}\), 而限制条件必不可少,单位向量是我们推导的前提 \(|| \mathbf{v} || = 1\), 否则没有这个限制最大化的话我们 \(\mathbf{v}\) 岂不是可以随便取大的。
最大化 \(||X^T\mathbf{v}||^2\) 也就是 最大化 \(\mathbf{v}^TXX^T\mathbf{v}\), 用格朗日乘数法,也就是
\[XX^T \mathbf{v} = \lambda \mathbf{v}\]
这个问题是求 \(XX^T\) 最大的 eigenvalue 的对应的 eigenvector.
4.1.2 物理方程
之前也写过, eigevalue, eigenvector 最早是为了解决微分方程出现的,比如最简单的考虑一个弹簧受力方程:
\[F = m \frac{d^2 \mathbf{x}}{dt} = -k \mathbf{x}\]
把微分算子写成 D:
\[ D^2 : f[\mathbf{x}] \to f[\mathbf{x}]\\ \mathbf{x} \mapsto D^2\mathbf{x} = \lambda \mathbf{x} \]
4.1.3 Quadratic Energy
有时候我们会有这样的 setup(比如图像分割):
Have:
- n items in a dataset
- \(w_{ij} ≥ 0\) similarity of items i and j
- \(w_{ij} = w_{ji}\)
Want: - \(x_{i}\) embedding on R
我们可以定义energy 方程:
\[ E(\mathbf{x}) = \sum_{ij} w_{ij} (x_i - x_j)^2 \]
我们想要最小化 \(E(\mathbf{x})\) 同时满足:
\[ ||\mathbf{x}||^2 = 1 \\ \mathbf{1} \cdot \mathbf{x} = 0 \]
加上这些限制是为了防止最小值平凡的取为0.
用格朗日乘数法:
\[ \begin{aligned} \Lambda &= \sum_{ij} w_{ij} (x_i - x_j)^2 - \lambda (\mathbf{x}^T \cdot \mathbf{x} - 1) - \mu (\mathbf{1} \cdot \mathbf{x}) {} \end{aligned} \]
最终化简为:
\[ E(\mathbf{x}) = \mathbf{x}^T(2A − 2W) \mathbf{x} \]
最终我们需要找到的是: 矩阵 2A − 2W 对应的第二小的特征值的特征向量, 为什么不是最小的呢?因为大概最小的特征值是0,对应的可能也是 \(\mathbf{0}\).
这个对应的更多资料和证明可以参见:
4.2 定义
4.2.1 特征值和特征向量
所以我们终于给出特征值和特征向量的定义了:
\[ A\mathbf{x} = \lambda \mathbf{x}\\ \lambda \in \mathbb{R} , A \in \mathbb{R}^{n \times n} \]
对于复数:
\[ A\mathbf{x} = \lambda \mathbf{x}\\ \lambda \in \mathbb{C} , \mathbf{x} \in \mathbb{C}^n \]
\(\lambda\) 是特征值, 而 \(\mathbf{x}\) 就是对应的特征向量
4.2.2 谱和谱半径
设 A 是 n × n 矩阵, 那么它的谱则是矩阵对应的特征向量。 而谱半径 ρ(A) 则是 \(\rho(A) = \max \left \{ |\lambda_1|, \cdots, |\lambda_n| \right \}\)
即矩阵A的谱半径等于矩阵A的特征值绝对值的最大值。 这句话好绕啊,还是看上面的数学式子比较明显。
4.2.3 有关特征值和特征向量的定理
- 每个 \(A \in \mathbb{R}^{n \times n}\) 至少有一个(复) 特征向量
- 不同的特征值对应的特征向量一定是线性无关
所以当然 A 最多可以有 n 个不同的特征值,毕竟它最多 rank 也是n, 有 n 个线性无关的column vector。
4.2.4 扩展到复域
首先我们知道复数的 \(z = a + ib \in \mathbb{C}\) 的 共轭是 \(\bar{z} = a - ib\) 。
共轭转置是 A (m x n) 满足:
\[{\displaystyle \left({\boldsymbol {A}}^{\mathrm {H} }\right)_{ij}={\overline {{\boldsymbol {A}}_{ji}}}} \]
以下写法都有:
\[{\boldsymbol {A}}^{\mathrm {H} }=\left({\overline {\boldsymbol {A}}}\right)^{\mathsf {T}}={\overline {{\boldsymbol {A}}^{\mathsf {T}}}}\]
埃尔米特矩阵( Hermitian) 矩阵是指:
\[{\displaystyle A{\text{ Hermitian}}\quad \iff \quad A= {A^H}}\]
埃尔米特矩阵的特征值都是实数,如果一个 A 只含实数,那么它是对称阵。
例如:
\[{\begin{bmatrix}3&2+i\\2-i&1\end{bmatrix}}\]
就是一个埃尔米特矩阵。 显然,埃尔米特矩阵主对角线上的元素都是实数的,其特征值也是实数。对于只包含实数元素的矩阵(实矩阵),如果它是对称阵,即所有元素关于主对角线对称,那么它也是埃尔米特矩阵。也就是说,实对称矩阵是埃尔米特矩阵的特例。
对于埃尔米特矩阵, 不同的特征值对应的不同的特征向量它们之间一定是正交的。
4.2.5 谱定理
假设 \(A \in \mathbb{C}^{n \times n}\) 是一个 埃尔米特矩阵(如果\(A \in\mathbf{R}^{n \times n}\), 假设它对称既可)。那么, A 会有 n 个 正交的特征向量 \(\mathbf{x}_1, \cdots, \mathbf{x}_n\) ,它们对应的特征值(当然,可能会重复) 则是 \(\lambda_1,\cdots, \lambda_n\).
这里其实会有一点疑惑,那就是重复的特征值不带来重复的特征向量么? 为什么它们还是可以 span \(\mathbb{R}^n\)。
然后我就开始想,比如 \(I\) :
明显 \(I\) 有 n 个重复的 eigenvalue 1, 不过 \(I\) 是明显 span \(\mathbb{R}^n\) 的。
对于更一般的情况,貌似总可以用 Gram–Schmidt 来求出基。重复的 eigenvalue 的 eigenvector span 的是 plane, 而不是我想象的共线啊。o(╯□╰)o
这里有一个解答:
谱定理非常重要,之前我多次写到过,比如傅里叶变换 中我写到过,傅里叶级数其实也就是可以看成谱定理,无非是:
- 把 \(\{1, \sin x, \cos x, \sin 2x, \cos2x, \cdots, \}\)看成空间中的基
- 然后展开成这组基的线性组合 \(f(x) = a_0/2 + \sum_{n = 1}^ \infty a_n \cos nx + b_n \sin nx\)
4.2.6 理论基础
再补充一点相关的理论基础:
\[A\mathbf{v} = \lambda \mathbf{v}\]
\[p(\lambda) = det(A - \lambda I) = 0\]
由代数基本定理(Fundamental theorem of algebra)我们知道 \(p(\lambda)\) 有 N 个解。这些解的解集也就是特征值的集合,有时也称为“谱”(Spectrum)。
代数基本定理: 任何一个非零的一元n次复系数多项式,都正好有n个复数根(重根视为多个根)。
因式分解:
\[p\left(\lambda\right)= (\lambda-\lambda_1)^{n_1}(\lambda-\lambda_2)^{n_2}\cdots(\lambda-\lambda_k)^{n_k} = 0 \!\ \]
其中:
\[\sum\limits_{i=1}^{k}{n_i} =N\]
对每一个特征值 \(\lambda_i\) ,我们都有下式成立:
\[ \left(\mathbf{A} - \lambda_i \mathbf{I}\right)\mathbf{v} = 0 \!\ \]
对每一个特征方程,都会有 \(m_i ( 1 \le m_i \le n_i)\) 个线性无关的解。这 \(m_i\) 个向量与一个特征值 \(\lambda_i\) 相对应。这里,整数 \(m_i\) 称为特征值 \(\lambda_i\) 的几何重数(geometric multiplicity),而 \(n_i\) 称为代数重数(algebraic multiplicity)。这里需要注意的是几何重数与代数重数可以相等,但也可以不相等。一种最简单的情况是 \(m_i = n_i = 1\)。特征向量的极大线性无关向量组中向量的个数可以由所有特征值的几何重数之和来确定。
这也是之前我们强调适用条件是 “具有线性独立特征向量(不一定是不同特征值)的方阵 A”,也就是看 n x n 的方阵 A 是否可以特征分解主要是看几何重数之和是否为 n 了。
4.3 计算
之前的文章中当然也写到过一些计算和它们的推导,比如:
\[A^k\mathbf{x} = \lambda^k\mathbf{x}\]
如果 A 可逆:
\[A^{-1}\mathbf{x} =\frac{1}{\lambda} \mathbf{x}\]
再来看一些别的,比如我们的 setup 是:
\[ A \in \mathbb{R} ^{n \times n} \\ \mathbf{x}_1, \cdots, \mathbf{x}_n \in \mathbb{R}^n \text{ eigenvector} \\ |\lambda_1| \ge |\lambda_2| \ge \cdots \ge |\lambda_n| \text{ eigenvalues} \]
根据谱定理,对于\(\mathbf{v} \in \mathbb{R}^n\), 我们有:
\[\mathbf{v} = c_1 \mathbf{x}_1 + \cdots + c_n\mathbf{x}_n\]
那么:
\[A^k\mathbf{v} = \lambda_1^k \bigg( c_1 \mathbf{x}_1 + (\frac{\lambda_2}{\lambda_1})^k c_2 \mathbf{x}_2 + \cdots + (\frac{\lambda_n}{\lambda_1})^k c_n\mathbf{x}_n \bigg)\]
4.3.1 最大的 eigenvalue 及对应的 eigenvector
如果 \(|\lambda_2| \le |\lambda_1|\) 有:
\[A^k \mathbf{v} = \lambda_1^k \mathbf{x}\]
所以比如我们取
\[\mathbf{v}_k = A \mathbf{v}_{k-1}\]
这样我们就可以算出来最大的 eigenvalue 对应的 eigenvector,当然我们需要注意可能 \(|\lambda_1| \ge 1\),所以我们最好做一个 normalize 操作:
\[\mathbf{w}_k = A \mathbf{v}_{k-1}\\ \mathbf{v}_k = \frac{\mathbf{w}_k}{|\mathbf{w}_k|} \]
这里的 norm 选哪个都所谓为,我们的重点只需要保证它不要无限制增长。
4.3.2 最小的 eigenvalue 及对应的 eigenvector
同样如果我们想要求出最小的 eigenvalue 对应的 eigenvector 我们可以这样操作:
\[\mathbf{w}_k = A^{-1} \mathbf{v}_{k-1}\\ \mathbf{v}_k = \frac{\mathbf{w}_k}{|\mathbf{w}_k|} \]
因为 \(A^{-1}\) 的特征值满足:
\[|\frac{1}{\lambda_1}| < |\frac{1}{\lambda_2}| < \cdots <|\frac{1}{\lambda_n}| \]
4.3.3 靠近 \(\sigma\)的 eigenvalue 及对应的 eigenvector
所以如果想要找到 靠近 \(\sigma\)的 eigenvalue 的 eigenvector :
\[\mathbf{v}_{k+1} = \frac{(A - \sigma I)^{-1} \mathbf{v}_k}{||(A - \sigma I)^{-1}\mathbf{v}_k||} \]
这个式子本质上跟上面找最小是一样的,我们是在找 \((A - \sigma I)\) 对应的最小的 eigenvector, 也就是这个 eigenvalue 需要靠近0, make sense.
4.3.4 根据 eigenvector 猜 eigenvalue
再来看一下问题的对立面,假设我们有一个 \(\mathbf{v}\) 非常靠近某个 eigenvector, 那么我们怎么求它对应的 eigenvalue 呢?
\[A\mathbf{v} \approx \lambda \mathbf{v}\]
这里我们要求的就是 \(\lambda\), 我们想做的就是:
\[ \text{arg min}_{\lambda}||A\mathbf{v} - \lambda \mathbf{v}||^2 \]
上面这个式子这种类型我们应该很熟悉了,展开,记住我们相求的是 \(\lambda\), 求导,最终可以写成是:
\[ \lambda = \frac{\mathbf{v}^T A \mathbf{v}}{||\mathbf{v}||^2} \]
上面这个式子叫做 瑞利熵(Rayleigh quotient)。
它给了我们一种算法,叫做 瑞利商迭代(Rayleigh quotient iteration)。
选择 \(\mathbf{v} \in R^n\) 为任意非零向量或者猜测一个特征向量。
迭代直至收敛:
- 计算对当前特征值的估计:\(\sigma_k = \frac{\mathbf{v}^T A \mathbf{v}}{||\mathbf{v}||^2}\)
- 求解 \(\mathbf{w}_k = (A - \sigma I)^{-1} \mathbf{v}_{k-1}\)
- \(\mathbf{v}_k = \frac{\mathbf{w}_k}{|\mathbf{w}_k|}\)
wikipedia 上有一个具体的例子: Rayleigh quotient iteration
上面我们写了如何计算最大的 eigenvalue, 最小的eigenvalue, 或者最靠近 \(\sigma\) 的。
4.3.5 All eigenevalue
那么如何算出所有的 eigenvalue 呢?先回到这个式子:
\[\mathbf{v} = c_1 \mathbf{x}_1 + \cdots + c_n\mathbf{x}_n\]
那么如果我们找到了一个和 \(\mathbf{x}\) 垂直的向量 \(\mathbf{v}_0\)
\[\mathbf{v}_0\cdot \mathbf{x}_1 = 0\]
那么如果我们把 \(\mathbf{v}\) 在 \(\mathbf{x}_1\) 方向上的投影减去, 令之为 \(\mathbf{v}_1\)
\[\mathbf{v}_1 = c_2 \mathbf{x}_2 + \cdots + c_n\mathbf{x}_n\]
\[A\mathbf{v_1} = \lambda_2 \bigg( c_2 \mathbf{x}_2 + \cdots + (\frac{\lambda_n}{\lambda_2}) c_n\mathbf{x}_n \bigg)\\ A^k\mathbf{v_1} = \lambda_2^k \bigg( c_2 \mathbf{x}_2 + \cdots + (\frac{\lambda_n}{\lambda_2})^k c_n\mathbf{x}_n \bigg)\]
这样不就可以继续算出 \(\mathbf{x}_2\) 了么?
这也提示了我们一种迭代法可以算出所有的 eigenvalue.
但是注意如果A 非对称,那么其特征向量不正交。
但是这个算法的前提是 \(\mathbf{x}_1, \cdots, \mathbf{x}_n\) 这些特征向量之间是正交的。
对于任意矩阵,其对应于不同特征值的特征向量线性无关,但不一定正交,而对于实对称矩阵,其对应于不同特征值的特征向量是相互正交的。
4.3.6 Householder 变换
如果A的特征向量不正交话我们可以用 Householder 变换配合来计算,假设我们有H如下:
\[H\mathbf{x}_1 = \mathbf{e}_1\]
\[ \begin{aligned} HAH^T\mathbf{e}_1 {} &= HAH\mathbf{e}_1 &H = H^T\\ &= HAHH\mathbf{x}_1 &H^2=I\\ &= HA\mathbf{x}_1 \\ &= \lambda_1H\mathbf{x}_1 \\ &= \lambda_1\mathbf{e}_1 \\ \end{aligned} \]
所以:
\[ HAH^T = \begin{bmatrix} \lambda_1 & b \\ 0 & B \end{bmatrix} \]
所以利用 H 可以计算出 \(\lambda_1\), 不过后续的还要迭代继续。
4.3.7 QR
如果:
\[A = QR\\ Q^{-1} = Q^{T} \\ Q^{-1}AQ = Q^TAQ = Q^T QR Q = RQ \]
这也就给我们了一个迭代算法
\[ A_1 = A \\ A_k = Q_kR_k\\ A_{k+1} = R_kQ_k \]
或者写成一句:
\[{\displaystyle A_{k+1}=R_{k}Q_{k}=Q_{k}^{-1}Q_{k}R_{k}Q_{k}=Q_{k}^{-1}A_{k}Q_{k}=Q_{k}^{\mathsf {T}}A_{k}Q_{k}}\]
\(A_k\) 系列总是相似的,有着相同的 eigenvalue, 而且这个方法具有数值稳定性。
具体参见: QR algorithm
具体计算我们依旧可以用 scipy.linalg 模块,有众多函数可选,比如: