Chapter 1 高斯消元法 {Gaussian elimination}

这篇文章只是尝试把高斯消元法写的更清楚一点。

考虑方程：

\[ A \mathbf{x} = \mathbf{b} \]

\(A \in R^{m \times n}, x \in R^n, b \in R^m\), 考虑A可逆，也就是以上方程只有唯一解。

1.1 数学

这实际上就是我们解矩阵方程组一般使用的方式，比如方程组是：

\[ a_{11}x_1 + a_{12}x_2 + \cdots + a_{1n}x_n = b_1 \\ a_{21}x_1 + a_{22}x_2 + \cdots + a_{2n}x_n = b_2 \\ \cdots \\ a_{m1}x_1 + a_{m2}x_2 + \cdots + a_{mn}x_n = b_m \\ \]

我们一般把它写成增广矩阵：

\[ \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} & b_1 \\ a_{21} & a_{22} & \cdots & a_{2n} & b_2 \\ & \cdots & \\ a_{m1} & a_{m2} & \cdots & a_{mn} & b_m \\ \end{bmatrix} \]

首先化简成阶梯型矩阵的形式：

\(row_1 / a_{11}\)
\(row_2 - k * row_1, k = \frac{a_{21}}{a_{11}}\)
…

这样第一列就化为 \(\begin{bmatrix} 1 \\ \vdots \\ 0 \end{bmatrix}\)

对于第二列我们可以继续类似的操作：

\(row_2 / (current)a_{22}\)
\(\cdots\)

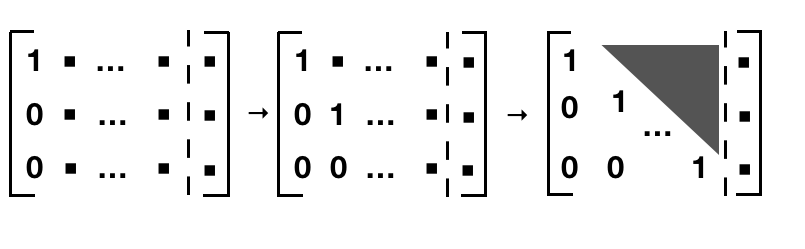
经过这些操作矩阵A变成这样的一个上三角矩阵。我们可以很容易的得到 \(x_m\) , 再往上回代就可以得到 \(x_1 \cdots x_m\)：

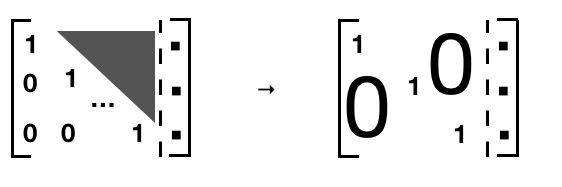
\(x_m\) get
\(row_{m-1} - k * row\)
\(\cdots\)

所以整个过程就只包括两个操作：

\(row * k\)
\(row_j + row_i * k\)

我们也可以用另一种观点来看上述过程，其实也是三步：

LU decomposition: A = LU ;
Forward substitution: solve Ly = b ;
Backward substitution: solve U x = y .

不过我们的前两步比较隐式和同时进行。

实际在计算机中计算，可能会出现的问题：

\(a_{11}\) 为0，不能除0
\(a_{11} \ll 1\)，除以一个很小很小的数会带来很多问题，比如overflow等

解决的办法就是行交换，把比较大的pivot放在前面。其实这个我们手动解 \(A\mathbf{x} = \mathbf{b}\) 的时候就会这样做，英文叫做 Gaussian elimination with partial pivoting (GEPP).

这里有一个具体的例子 https://web.mit.edu/10.001/Web/Course_Notes/GaussElimPivoting.html

这个英文就暗示了还有别的方法，因为这是 partial pivoting，还有一种 total pivoting，就是不仅仅只考虑行的交换，比如我们为了得到最大的\(a_{11}\), 我们也把列的交换也考虑上。

因为有行交换的原因，所以严格写会是：

\[ A = PLU \]

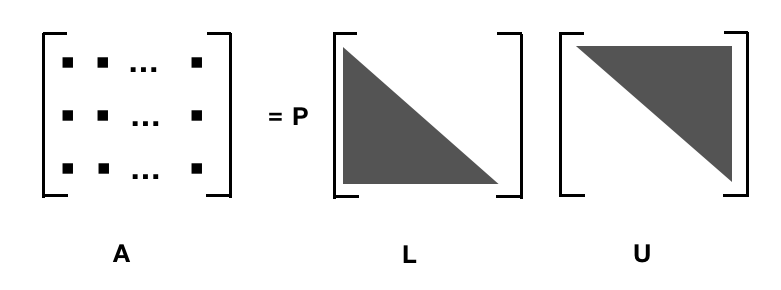
同样也可以用另一种观点来看这个方法的正确性：

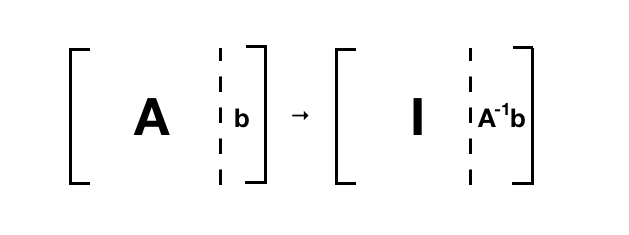
不过我们并没有来算出 \(A^{-1}\)

1.2 计算

实际中，对于不是极其繁琐的有解线性方程组可以直接调库，比如直接用 scipy.linalg.solve 来帮助我们解方程, 一般来说，它会快于我们计算 \(A^{-1}\)，然后 \(A^{-1}b\)。

计算

\[ \begin{cases} 2x_1 + 4x_2 - 2x_3 = 2 \\ x_1 - 3x_2 - 3x_3 = -1\\ 4x_1 + 2x_2 + 2x_3 = 3 \end{cases} \]

import numpy as np
from scipy import linalg

a = np.array([[2 ,4 ,-2],
              [1, -3, -3],
              [4, 2, 2,]])
b = np.array([2, -1, 3])

x = linalg.solve(a, b)
np.dot(a, x) # array([ 2., -1.,  3.])
x # array([0.5       , 0.33333333, 0.16666667])

array([0.5       , 0.33333333, 0.16666667])

我们的解答还是很接近数值解的：

\[ \begin{cases} x_1 = 1/2 \\ x_2 = 1/3\\ x_3 = 1/6 \end{cases} \]

更多操作，比如 lu 分解可以查看文档 scipy.linalg.lu