Chapter 16 数值积分和微分{Numerial Intergration}

16.1 积分

针对 $f: \mathbb{R} \to \mathbb{R}$

16.1.1 黎曼和

记得我第一次看黎曼和/黎曼积分的时候觉得真是有意思，觉得这个东西很不言自明，我们推推导积分的时候从有限小到无限小，而当我们为了计算机计算，又从无穷小到可衡量的有限小。有意思。

积分也就是求和。而且觉得这一切都和中值定理有着千丝万缕的联系，o(╯□╰)o ：

对一个在闭区间 [a,b]有定义的实值函数f, f关于取样分割$ x_{0},,x_{n}、t_{0},,t_{n-1}$ 的黎曼和（积分和）定义为以下和

\[ \sum _{i=0}^{n-1}f(t_{i})(x_{i+1}-x_{i}) \]

和式中的每一项是子区间长度 $ x_{i+1}-x_{i}$ 与在 $t_{i}$ 处的函数值 $f(t_{i})$ 的乘积。直观地说，就是以标记点 $t_{i}$ 到 X轴的距离为高，以分割的子区间为长的矩形的面积。

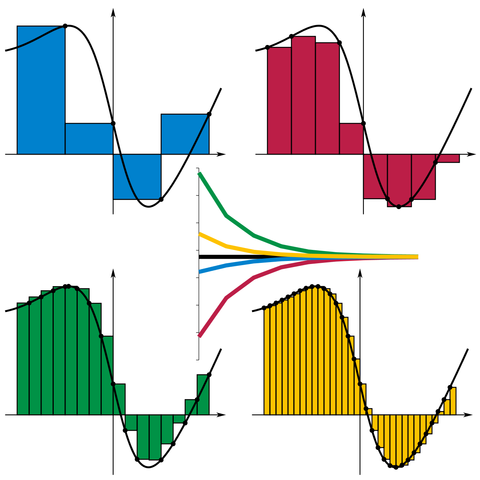
图片来自wikipedia

在上图中， $f(t_i)$ 选择分别为左端、右端、极小值、极大值。

16.1.2 梯形法则

在一个‘小区间’我们就能玩出很多花样：

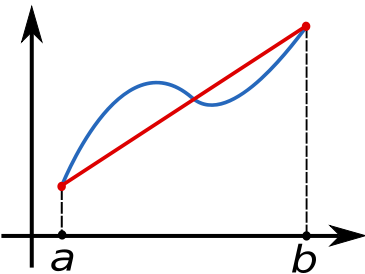
比如我们如果取两端来估算面积的话：

\[{\displaystyle \int \limits _{a}^{b}f(x)dx\approx {\frac {b-a}{2}}[f(a)+f(b)]}\]

我们也可以取区间中点的高度来估计面积：

\[{\displaystyle \int \limits _{a}^{b}f(x)dx\approx (b-a)f({\frac {a+b}{2}})}\]

以上都被称为梯形法则（Trapezoidal rule），这里可以是整个函数，也可以只是一个小区间，我们可以用黎曼和来对待小区间：

分割许多小区间
把小区间加起来

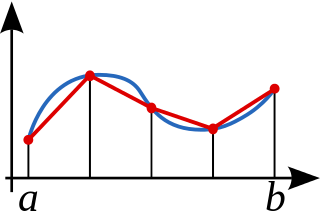
16.1.3 辛普森法则

辛普森法则（Simpson’s rule）是一种数值积分方法，是牛顿-寇次公式的特殊形式，以二次曲线逼近的方式取代矩形或梯形积分公式，以求得定积分的数值近似解。其近似值如下：

\[\int_{a}^{b} f(x) \, dx \approx \frac{b-a}{6}\left[f(a) + 4f\left(\frac{a+b}{2}\right)+f(b)\right]\]

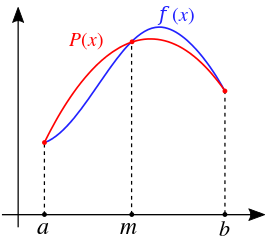
辛普森法则可以令 $f(x) = A x^2 + Bx + C$ 然后推导出来。

同样也可以分割小区间然后求和。

实际上上面两种无非是采取了不不同的近似，梯形法则使用直线来近似原函数，辛普森法则使用二次曲线来近似原函数。它们都是牛顿-柯特斯公式（Newton-Cotes rule / Newton-Cotes formula）的特殊形式。

16.1.4 牛顿-柯特斯公式

还有一些有趣的看法，比如我们始终是利用 n 个离散的点的值来得到积分结果 - 一个数字，那么积分总可以写成这样：

\[\int _{a}^{b}f(x)\,dx\approx \sum _{{i=0}}^{n}w_{i}\,f(x_{i})\]

这种看法的原理是：

假设已知 $f(x_{0}),f(x_{1}),\dots ,f(x_{n})$ 的值。
以n+1点进行插值，求得对应 f(x)的拉格朗日多项式。
对该n次的多项式求积。

该积分便可以作为 $\int _{a}^{b}f(x)\,dx$ 的近似，而由于该拉格朗日多项式的系数都是常数（由n决定其值），所以积函数的系数（即 $w_{i}$）都是常数。

或者就这样写：

\[ \begin{aligned} \int_a^b f(x)dx &= \int_a^b \bigg[ \sum_i a_i \phi_i(x)\bigg] dx \\ &=\sum_i a_i \bigg[ \int_a^b \phi_i(x)\bigg] dx\\ &= \sum_i c_i a_i, \text{ for } c_i \equiv \int_a^b \phi_i(x) dx \end{aligned} \]

然后我们就可以写出方程组：

\[ w_1 \cdot 1 + w_2 \cdot 2 + \cdots + w_n \cdot 1 = \int_a^b 1dx = b - a \\ w_1 \cdot x_1 + w_2 \cdot x_2 + \cdots + w_n \cdot x_n = \int_a^b xdx = (b^2 - a^2)/2 \\ \vdots \\ w_1 \cdot x_1^{n-1} + w_2 \cdot x_2^{n-1} + \cdots + w_n \cdot x_n^{n-1} = \int_a^b x^{n-1}dx = (b^n - a^n)/n \\ \]

然后也就是一个解线性方程组的问题。

这个方法明显会有高阶多项式震荡的厉害的龙格现象，我还是更喜欢拆小区间，然后再组合小区间的做法。

16.1.5 精确度

用拆小区间再复合梯形法则的精确度是 $O(\Delta x^3)$, 辛普森的精确度是 $O(\Delta x^4)$

针对 $f: \mathbb{R}^k \to \mathbb{R}$，好像针对多元函数，蒙特卡洛积分比较常见/用一点。

16.2 微分

关于微分，我们首先也可以用插值类似的思想来看

\[ f'(x) = \sum_i a_i \phi_i'(x) \]

这是有限元的思想。

当然更简单的就是我们直接从定义入手：

\[ f'(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h} \]

选择比较小的h，得到前向差分公式：

\[ f'(x) \approx \frac{f(x+h) - f(x)}{h} \]

也可以从 x 向后得到后向差分公式：

\[ f'(x) \approx \frac{f(x) - f(x-h)}{h} \]

以上两个式子本质都是用的泰勒展开：

\[ f(x+h) = f(x) + f'(x) h + \frac{1}{2} f''(x) h^2 + \cdots \]

精度为 O(h):

\[ f'(x) = \frac{f(x+h) - f(x)}{h} + O(h) \]

或者我们可以用下面的办法展开：

\[ f(x+h) = f(x) + f'(x) h + \frac{1}{2} f''(x) h^2 + \frac{1}{6}f'''(x)h^3 + \cdots \tag{1}\\ \]

\[ f(x-h) = f(x) - f'(x) h + \frac{1}{2} f''(x) h^2 - \frac{1}{6}f'''(x)h^3 + \cdots \tag{2} \] 上下两式相减：

\[ f(x+h) - f(x -h) = 2f'(x) + \frac{1}{3}f'''(x)h^3 + \cdots \]

这叫做中点差分公式，精度是 $O(h^2)$

\[ f'(x) \approx \frac{f(x+h) - f(x-h)}{2h} \]

我们也可以用（1），（2）式得到二阶导数的 O(h) 中点差分公式：

\[ f''(x) \approx \frac{f(x+h) - 2f(x) + f(x-h)}{h^2} \]

我们可以利用理查德森外推法来提高二阶导的精度：

\[ D(h) = \frac{f(x+h) - f(x)}{h} = f'(x) + \frac{1}{2} f''(x) h + O(h^2) \]

对于任意 $\alpha$ ，我们可以有 $D(h), D(\alpha h)$:

\[ D(h) = f'(x) + \frac{1}{2} f''(x) h + O(h^2) \\ D(\alpha h) = f'(x) + \frac{1}{2} f''(x) \alpha h + O(h^2) \\ \]

写成矩阵形式：

\[ \begin{pmatrix} D(h) \\ D(\alpha h) \end{pmatrix} = \begin{pmatrix} 1 & \frac{1}{2}h \\ 1 & \frac{1}{2}\alpha h \end{pmatrix}\begin{pmatrix} f'(x) \\ f''(x) \end{pmatrix} + O(h^2) \]

\[ \begin{pmatrix} f'(x) \\ f''(x) \end{pmatrix} = \begin{pmatrix} 1 & \frac{1}{2}h \\ 1 & \frac{1}{2}\alpha h \end{pmatrix}^{-1} \begin{pmatrix} D(h) \\ D(\alpha h) \end{pmatrix} + O(h^2) \]

这样可以以解出精度为 $O(h^2)$ 的 f’(x):

\[ f'(x) = \frac{1}{1- \alpha}(-\alpha D(h) + D(\alpha h)) + O(h^2) \]

参考：

数值积分和微分当然非常有用，中文翻译的差分也很合适，其实数值积分和微分就是求和和差分。这当然很重要，有了积分和微分（求和和差分）才能帮我们把一些数学方程/模型方便的用到计算机上。

比如渲染领域的蒙特卡洛积分。

然后发现 Scipy 也提供 integrate，可以查看： SciPy求函数的积分